张益唐新成果直播 开局写下ac-bd=(a b)c-(c d)b：这次看得懂？

张益唐在北京大学学术讨论，各个平台超10万人在线观看，一起见证历史时间！

张益唐攻破朗道-西格尔零点猜测消息，持续触动心弦。

这事也由于毕业论文在arXiv上发布，及其他自己首次公开直播介绍成效，而又被引向深入。

一位学数学的好朋友表明，“今日睁开眼睛第一件事，是看张益唐的直播间”。

在此次声明中，张益唐再度提及了“海底捞针”。

有人说他证实孪生素数猜想如同海底捞针，他本人则感觉朗道-西格尔零点猜测的相关证明更像是海底捞针。

此次的学术讨论，让张益唐还有机会深层次阐述了他这个“被闪电击中两次的人”到底是怎么“海底捞针”的。

据浙江大学数学教授蔡天新表露，张益唐的硕士生导师、中科院院士潘承彪听完报告后评价到：

听完益唐说的念头比较清楚，这也是一个重要的筛法新发展理念，也有很大发展前景，可以实现起来也是难。

从海底捞针到独辟蹊径

朗道-西格尔零点猜测，是理论黎曼猜想的一个独特方式。

实质上这种情况要这样了解：一位数学家们需要证实，狄利克雷的L函数公式根本不存在一个很接近1的零点（即朗道-西格尔零点）。

在朗道-西格尔零点猜测中，L函数的实零点与1之间的距离应是：

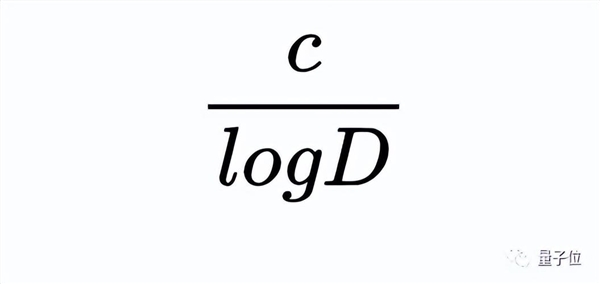
面对这些难题，一开始，张益唐的想法是这种。

最先，结构一个实数编码序列 {xn}，如果出现朗道-西格尔零点，就发布xn≥0。

那样只需证实有xn＜0，朗道-西格尔零点就根本不存在。

但根据塞尔伯格筛法，这种情况就会变成，要寻找一组实数编码序列 {ξn}，促使：

张益唐描述，找这一ξn，就是一个海底捞针的一个过程。直到他就把深海的现象都摸清楚了，都没找到这一根针来。

但是到此刻张益唐发觉，即便没有这一根“针”，他也能解决这些问题。

这一新点子，被归纳为一个非常基本的算式：ac-bd=(a b)c-(c d)b。

进行而言，便是张益唐引进了2组编码序列 {an bn} 和 {cn dn}。

他证实，xn与 (an bn)^2的相乘总和很接近0。第二组编码序列同样。

此刻，假设xn≥0，根据 ac-bd=(a b)c-(c d)b，就能发布下列结论：

然后依据柯西不等式，可能两边算式的确界，就能发现，这一不等式的左侧比右侧大，并不是设立的。

那样，张益唐就获得了3个出题，最终根据证实3个出题，获得实零点与1间的距离应低于：

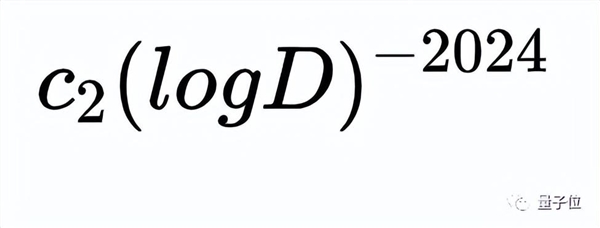
这一部分更准确的小细节，在文章的第二节。

改善延用70年数论方式

省掉许多繁杂关键点，张益唐仅用了40分钟就最好以易懂的语言表达阐述了自身晦涩的探索。

下面的观众问答环节，好多人关注这一成效到底可用在哪儿？

在之前过程中张益唐曾称，比孪生素数猜想的价值更高。

朗道-西格尔零点猜测有些像黎曼猜想那般，它一处理，一百个猜测都变成定律了。

此次的学术讨论使他能把话题讨论更加深入到对数论产生的影响。

张益唐觉得对于许多数论难题来讲，朗道-西格尔零点是一个短板。超越过这个短板，也会有很多运用出去。

例如“素数在等差级数里的遍布”是一个长期难以解决问题。

假如朗道西格尔零点存有，就表明一些等差级数里素数会多得很，一些中会非常少。

但我这样的结果出来之后，最少将这个克服了。

张益唐还实际说了数论的两大支系，解析数论与代数数论。

牵涉到解析数论，那么什么地方都是得使用这一。

代数数论中二次域的类数难题，会给出一个比较强的结论。

除开研究结果以外，张益唐此次需要用到的方式一样极其重要。

1950年前后左右，阿特勒·塞尔伯格（Atle Selberg）明确提出塞尔伯格筛法，变成数论科学研究中的关键专用工具并沿用至今。

在很长一段时间里，此方法全是“初始可能在一个小区间里素数遍布以上界”的唯一方式，曾使哥德巴赫猜想前行一大步，张益唐处理孪生素数猜想思路也受此启迪。

这一次张益唐不断地“海底捞针”，尽管没有捞着塞尔伯格筛法中的那根“针”，但总算是设计方案出新方法。

新的方法不依赖“求二次型极大值”，除开用以朗道-西格尔零点猜测外，以及望用以别的数论难题。

张益唐自己表明，他正思索能不能用新的方法改善以前的孪生素数猜想结论。

这也是可以选择的，我会往这方面去想。

张益唐在他孪生素数猜想文章中验证了“存有无限多间隔低于七千万的邻近素数对”。

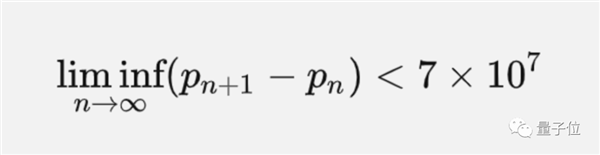
七千万这个数，之后在世界上一位数学家签约合作Polymath Project 8新项目努力下早已变小到246。

应用新的方法，这一间隔有希望再次向着终极目标2前行。

与此同时，也代表着朗道-西格尔零点猜测的结果就是能够改善的。

张益唐为敬礼他作出成效的这一年，把对应的数据当选2022，这一次的终极目标乃是1。

也有人调侃说，假如他可在2021年进行证实，那然后就比得上如今更准确一点。

在此次汇报上，张益唐表明靠现在这方式该是可以做到好几百。

……仅仅我没有去做。可是需到1现阶段用这种方法还远远不够的。

现阶段这篇文章新毕业论文还没有经过同行评议，尚需学界认证其结果。

而一旦毕业论文被认可正确，可以想见是指下面物理学界还会在他的工作前提下持续向1迈进。

最终，在讨论中还有一些人注意到了张益唐的年纪。

一旦毕业论文被认证，67岁张益唐就打破数学名人哈代“数学是年轻人手机游戏”这一观点。

在此前在接受采访时，张益唐就数次表达自己不认同这一说”。

对他那个东西并不是十分注意，我觉得好像跟我也没直接影响一样，我并没有受这些东西产生的影响。

现在他验证了一个新的猜测，也以实际行动证明了自己得话。

张益唐零点猜测毕业论文：https://arxiv.org/abs/2211.02515